高考文数立体几何-立体几何高考题文科

1.文科生在高考中能用向量解立体几何吗？

2.高中文科数学高考范围有哪些？

3.福建省文科数学高考共建立体几何用向量的方法给分不？

4.求高考文科数学立体几何题十二道！

文科生在高考中能用向量解立体几何吗？

不管是什么证明题，只要不限定证明的方法，用什么方法都是可以的，尤其是高考，即使你用的是大学才学的方法，都可以。

不直接把这个内容简单的知识编入文科教材中？其实向量法在我来说是很难掌握好的，可能教育局的人认为文科生不需要掌握它吧。

全国的文科生都由老师单独补了向量法解立几？立几不一定非得用向量法，而且高考好像也没限定一定要用吧？

合理的话，不就等于把文科生当理科生教？学生可以自学的，只要有能力，也能学好。

高中文科数学高考范围有哪些？

高中文科数学高考范围有三角函数、向量、概率与统计、立体几何、数列、圆锥曲线、函数、导数与不等式等。

1、三角函数、向量、解三角形

(1)三角函数画图、性质、三角恒等变换、和与差公式。(2)向量的工具性。(3)正弦定理、余弦定理、解三角形背景。

2、概率与统计

(1)古典概型。(2)茎叶图。(3)直方图。(4)回归方程(2x2列联表)。(5)(理)概率分布、期望、方差、排列组合。

3、立体几何

(1)平行。(2)垂直。(3)角a:异面直线角b:(理)二面角、线面角。(4)利用三视图计算面积与体积。

4、数列

(1)等差数列、等比数列、递推数列是考查的热点，数列通项、数列前n项的和以及二者之间的关系。(2)错位相减法、裂项求和法。(3)应用题。

5、圆锥曲线(椭圆)与圆

(1)椭圆为主线，强调圆锥曲线与直线的位置关系，突出韦达定理或差值法。(2)圆的方程，圆与直线的位置关系。

6、函数、导数与不等式

(1)函数是该题型的主体：三次函数，指数函数，对数函数及其复合函数。(2)利用基本不等式、对勾函数性质。

三角函数/数列：一般全国卷第17题会考三角函数或数列题。数列是最简单的题目，或许你觉得它难，但它能放在第一道大题的位置，就说明你不应该丢分。

概率：一般全国卷第18题会考概率题。概率题相对比较简单，也是必须得分的题，主要还是对作图和识图能力考查比较多。

解析几何：一般全国卷第20题会考解析几何题。解析几何也不是难题，只要大家平时努力，这些题目都算是相对简单的。

福建省文科数学高考共建立体几何用向量的方法给分不？

给分

但空间向量有特殊之处，如果高考题出的巧那么就很难建出来

空间向量没有步骤分，坐标算对了给分，没得出结果那一小问直接没分

而且你注意要区别左手系和右手系的问题

空间向量适合证不显著甚至要添线的平行和垂直问题

求高考文科数学立体几何题十二道！

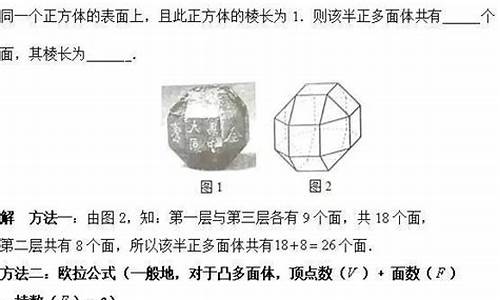
1、（2010年辽宁卷）已知 是球 表面上的点， ， ， ， ，则球 表面积等于

（A）4 （B）3 （C）2 （D）

2、（2010年辽宁卷）

如图，棱柱 的侧面 是菱形，

（Ⅰ）证明：平面 平面 ；

（Ⅱ）设 是 上的点，且 平面 ，求 的值。

3、（2010年北京卷）一个长方体去掉一个小长方体，所得几何体的正视图与侧（左）视图分别如右图所示，则该集合体的俯视图为：

4、（2010年北京卷）如图，正方形ABCD和四边形ACEF所在的平面互相垂直。

EF//AC，AB= ,CE=EF=1

（Ⅰ）求证：AF//平面BDE；

（Ⅱ）求证：CF⊥平面BDF;

5、（2010年山东卷）在空间，下列命题正确的是

（A）平行直线的平行投影重合 (B)平行于同一直线的两个平面

（C）垂直于同一平面的两个平面平行 （D）垂直于同一平面的两个平面平行

6、（2010年山东卷）

在如图所示的几何体中，四边形 是正方形，

, , 分别为 、 的中点，

且 .

(Ⅰ) 求证：平面 ;

(Ⅱ)求三棱锥 .

7、（2010年陕西卷）若某空间几何体的三视图如图所示，则该几何体的体积是

（A）2 （B）1

（C） （D）

8、（2010年陕西卷）如图，在四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB,PC的中点.

(Ⅰ)证明：EF‖平面PAD；

(Ⅱ)求三棱锥E—ABC的体积V.

9、（2010年上海卷）已知四棱椎 的底面是边长为6 的正方形，侧棱 底面 ，且 ，则该四棱椎的体积是 。

10、（2010年天津卷）一个几何体的三视图如图所示，则这个几何体的体积为 。

11、（2010年全国卷）设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上，则该球的表面积为

（A）3 a2 （B）6 a2 （C）12 a2 （D） 24 a2

12、（2010年全国卷）一个几何体的正视图为一个三角形，则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)

①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥 ⑥圆柱

13、（2010年全国卷）如图，已知四棱锥 的底面为等腰梯形， ‖ , ,垂足为 ， 是四棱锥的高。

（Ⅰ）证明：平面 平面 ;

（Ⅱ）若 , 60°,求四棱锥 的体积。

14、（2010年浙江卷）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是

（A） cm3 （B） cm3

（C） cm3 （D） cm3

答案：

1、 A

2、解：（Ⅰ）因为侧面BCC1B1是菱形，所以

又已知

所又 平面A1BC1，又 平面AB1C ，

所以平面 平面A1BC1 .

（Ⅱ）设BC1交B1C于点E，连结DE，

则DE是平面A1BC1与平面B1CD的交线，

因为A1B//平面B1CD，所以A1B//DE.

又E是BC1的中点，所以D为A1C1的中点.

即A1D：DC1=1.

3、C

4、证明：（Ⅰ）设AC于BD交于点G。因为EF‖,且EF=1，= =1

所以四边形EF为平行四边形

所以AF‖EG

因为EG 平面BDE,AF 平面BDE,

所以AF‖平面BDE

（Ⅱ）连接FG。因为EF‖CG,EF=CG=1,且CE=1,

所以平行四边形CEFG为菱形。

所以CF⊥EG.

因为四边形ABCD为正方形，

所以BD⊥AC.

又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,

所以BD⊥平面ACEF.

所以CF⊥BD.

又BD∩EG=G,

所以CF⊥平面BDE.

5、D

6、解析（I） 证明：由已知MA 平面ABCD，PD ‖MA，

所以 PD∈平面ABCD

又 BC ∈ 平面ABCD，

因为 四边形ABCD为正方形，

所以 PD⊥ BC

又 PD∩DC=D，

因此 BC⊥平面PDC

在△PBC中，因为G平分为PC的中点，

所以 GF‖BC[

因此 GF⊥平面PDC

又 GF ∈平面EFG，

所以 平面EFG⊥ 平面PDC.

（Ⅱ ）解：因为PD⊥平面ABCD,四边形ABCD为正方形，不妨设M A=1，

则 PD=AD=2，AB CD

所以 Vp-ABCD=1/3S正方形ABCD，PD=8/3

由于 DA⊥面MAB的距离

所以 DA即为点P到平面MAB的距离，

三棱锥 Vp-MAB=1/3×1/2×1×2×2=2/3 ，所以 Vp-MAB：Vp-ABCD=1:4。

7、B

8、解： (Ⅰ)在△PBC中，E，F分别是PB，PC的中点，∴EF‖BC.

又BC‖AD,∴EF‖AD,

又∵AD 平面PAD,EF 平面PAD,

∴EF‖平面PAD.

(Ⅱ)连接AE,AC,EC,过E作EG‖PA交AB于点G,

则BG⊥平面ABCD,且EG= PA.

在△PAB中，AD=AB, PAB°,BP=2,∴AP=AB= ,EG= .

∴S△ABC= AB?BC= × ×2= ,

∴VE-ABC= S△ABC?EG= × × = .

9、96 10、3 11、B 12、①②③⑤

13、解：(1)因为PH是四棱锥P-ABCD的高。

所以AC PH,又AC BD,PH,BD都在平PHD内,且PH BD=H.

所以AC 平面PBD.

故平面PAC平面PBD.

(2)因为ABCD为等腰梯形，

AB CD,AC BD,AB= .

所以HA=HB= .

因为 APB= ADR=600

所以PA=PB= ,HD=HC=1.

可得PH= .

等腰梯形ABCD的面积为S= AC x BD = 2+ .

所以四棱锥的体积为V= x（2+ ）x =

14、B