圆锥曲线在高考题_圆锥曲线高考题讲解

1.数学高考圆锥曲线题目 ， 谁能帮我解一下 最好能详细点，能迁移一下？

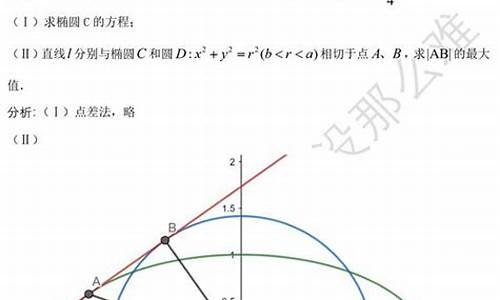
你好，很高兴为你解答这个问题。

高考当中一般圆锥曲线大题，作为倒数第二道或者倒数第一道压轴大题。

我们以新课标全国卷为例。

圆锥曲线大题出在第20题。

具体题目，第一问往往是基础知识的考察，即离心率，标准方程，不同圆锥曲线中a，b，c，的简单识别计算。难度较小。

第二问，我们一般叫做圆锥曲线和直线的位置关系。这是近些年来的主流考法。用代数的角度，解决几何问题。

圆锥曲线分作，椭圆，抛物线，双曲线，圆。高考当中出现的圆锥曲线，除了选填当中可能出现圆，大题当中，主要是椭圆，偶尔有抛物线，很少出现双曲线，不出现圆。希望可以帮到你

数学高考圆锥曲线题目 ， 谁能帮我解一下 最好能详细点，能迁移一下？

圆锥曲线的综合问题：

1、圆锥曲线的范围问题有两种常用方法：?

（1）寻找合理的不等式，常见有△＞0和弦的中点在曲线内部；?

（2）所求量可表示为另一变量的函数，求函数的值域。?

2、圆锥曲线的最值、定值及过定点等难点问题。

(1)从几何角度来看，直线和圆锥曲线有三种位置关系：相离、相切和相交，相离是直线和圆锥曲线没有公共点，相切是直线和圆锥曲线有唯一公共点，相交是直线与圆锥曲线有两个不同的公共点，并特别注意直线与双曲线、抛物线有唯一公共点时，并不一定是相切，如直线与双曲线的渐近线平行时，与双曲线有唯一公共点，但这时直线与双曲线相交；直线平行（重合）于抛物线的对称轴时，与抛物线有唯一公共点，但这时直线与抛物线相交，故直线与双曲线、抛物线有唯一公共点时可能是相切，也可能是相交，直线与这两种曲线相交，可能有两个交点，也可能有一个交点，从而不要以公共点的个数来判断直线与曲线的位置关系，但由位置关系可以确定公共点的个数．

(2)从代数角度来看，可以根据直线方程和圆锥曲线方程组成的方程组解的个数确定位置关系．设直线l的方程与圆锥曲线方程联立得到ax2+bx+c=0．

①若a=0，当圆锥曲线是双曲线时，直线l与双曲线的渐近线平行或重合；当圆锥曲线是抛物线时，直线l与抛物线的对称轴平行或重合．

②若

当Δ>0时，直线和圆锥曲线相交于不同两点，相交．

当Δ=0时，直线和圆锥曲线相切于一点，相切．

当Δ<0时，直线和圆锥曲线没有公共点，相离．

直线与圆锥曲线相交的弦长公式：

若直线l与圆锥曲线F(x，y)=0相交于A，B两点，求弦AB的长可用下列两种方法：

(1)求交点法：把直线的方程与圆锥曲线的方程联立，解得点A，B的坐标，然后用两点间距离公式，便得到弦AB的长，一般来说，这种方法较为麻烦．

(2)韦达定理法：

(1)从几何角度来看，直线和圆锥曲线有三种位置关系：相离、相切和相交，相离是直线和圆锥曲线没有公共点，相切是直线和圆锥曲线有唯一公共点，相交是直线与圆锥曲线有两个不同的公共点，并特别注意直线与双曲线、抛物线有唯一公共点时，并不一定是相切，如直线与双曲线的渐近线平行时，与双曲线有唯一公共点，但这时直线与双曲线相交；直线平行（重合）于抛物线的对称轴时，与抛物线有唯一公共点，但这时直线与抛物线相交，故直线与双曲线、抛物线有唯一公共点时可能是相切，也可能是相交，直线与这两种曲线相交，可能有两个交点，也可能有一个交点，从而不要以公共点的个数来判断直线与曲线的位置关系，但由位置关系可以确定公共点的个数．

(2)从代数角度来看，可以根据直线方程和圆锥曲线方程组成的方程组解的个数确定位置关系．设直线l的方程与圆锥曲线方程联立得到ax2+bx+c=0．

①若a=0，当圆锥曲线是双曲线时，直线l与双曲线的渐近线平行或重合；当圆锥曲线是抛物线时，直线l与抛物线的对称轴平行或重合．

②若

当Δ>0时，直线和圆锥曲线相交于不同两点，相交．

当Δ=0时，直线和圆锥曲线相切于一点，相切．

当Δ<0时，直线和圆锥曲线没有公共点，相离．

直线与圆锥曲线相交的弦长公式：

若直线l与圆锥曲线F(x，y)=0相交于A，B两点，求弦AB的长可用下列两种方法：

(1)求交点法：把直线的方程与圆锥曲线的方程联立，解得点A，B的坐标，然后用两点间距离公式，便得到弦AB的长，一般来说，这种方法较为麻烦．

(2)韦达定理法：

不求交点坐标，可用韦达定理求解．若直线l的方程用y=kx+m或x=n表示．

右不等号：λ＋1／λ＋2<16/3解得1/3<λ<3

左不等号：4<λ＋1／λ＋2解得λ不等于1

综上:1/3<λ<1

然后“FG=λFH,点G在点F ,H 之间”易得：0<λ<1 （0</FG/</FH/模长）

注意充分利用条件，抓住题干中的每一句话（尤其是圆锥曲线和应用题）！！！