高考绝对值不等式的题目,高考绝对值不等式

1.有关绝对值的不等式

2.绝对值不等式的解法

3.含有两个绝对值的不等式，咋解啊

4.带绝对值的不等式怎么算

5.含绝对值的不等式恒成立问题！急！

6.绝对值不等式性质及公式

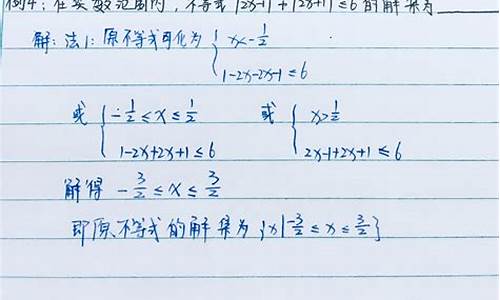
先设定x的范围，然后直接去绝对值。如同解分段函数一般

本题如下：

当x≤-3时

-（x+3)-(2-x)=-5≥3，不成立；∴当x≤-3时，不等式无解；

当-3＜x≤2时

（x+3)-(2-x)=2x+1≥3，解出x≥1；综合-3＜x≤2，可知1≤x≤2；

当x＞2时

（x+3)-(x-2)=5≥3，恒有解；

综上所述，x≥1为该不等式的解集

有关绝对值的不等式

一、 绝对值定义法

对于一些简单的，一侧为常数的含不等式绝对值，直接用绝对值定义即可，?

1、如|x| < a在数轴上表示出来。利用数轴可将解集表示为?a< x < a

2、|x| ≥ a同理可在数轴上表示出来，因此可得到解集为x≥ a或x≤ a

3、|ax +b| ≥ c型，利用绝对值性质化为不等式组?c ≤ ax + b ≤ c，再解不等式组。

二、平方法

对于不等式两边都是绝对值时，可将不等式两边同时平方。

解不等式 |x+ 3| > |x? 1|将等式两边同时平方为(x + 3)2 > (x ? 1)2得到x2 + 6x + 9 > x2 ? 2x + 1之后解不等式即可，解得x > ?1

三、零点分段法

对于不等式中含有有两个及以上绝对值，且含有常数项时，一般使用零点分段法。例 解不等式|x + 1| + |x ? 3| > 5

在数轴上可以看出，数轴可以分成x < ?1,?1 ≤ x < 3, x ≥ 3三个区间，由此进行分类讨论。

当x < ?1时，因为x + 1 < 0, x ? 3 < 0所以不等式化为 ?x? 1 ?x + 3 > 5解得x < ?322．当?1 ≤x < 3时， 因为x + 1 > 0,x? 3 < 0所以不等式化为x + 1 ? x + 3 > 5无解。

当 x ≥ 3时 因为x + 1 > 0 ,x ? 3 > 0所以不等式化为x + 1 + x? 3 > 5解得x >72综上所述，不等式的解为x < ?32或x >72。

扩展资料

1、实数的绝对值的概念

(1)|a|的几何意义

|a|表示数轴上实数a对应的点与原点之间的距离.

(2)两个重要性质

①(ⅰ)|ab|=|a||b|

②|a|<|b|?a2<b2

(3)|x-a|的几何意义:数轴上实数x对应的点与实数a对应的点之间的距离,或数轴上表示x-a的点到原点的距离.

(4)|x+a|的几何意义:数轴上实数x对应的点与实数-a对应的点之间的距离,或数轴上表示x+a的点到原点的距离。

2、绝对值不等式定理

(1)定理：对任意实数a和b,有|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.

(2)定理的另一种形式：对任意实数a和b,有|a-b|≤|a|+|b|,当且仅当ab≤0时,等号成立.

绝对值不等式定理的完整形式：|a|-|b|≤|a±b|≤|a|+|b|.

其中,(1)|a+b|=|a|-|b|成立的条件是ab≤0,且|a|≥|b|;

(2)|a+b|=|a|+|b|成立的条件是ab≥0;

(3)|a-b|=|a|-|b|成立的条件是ab≥0,且|a|≥|b|;

(4)|a-b|=|a|+|b|成立的条件是ab≤0.

绝对值不等式的解法

其实这是三角形不等式：||a|-|b||≤|a±b|≤|a|+|b|

证明：

先证|a+b|≤|a|+|b|，即：-|a|-|b|≤a+b≤|a|+|b|

因为：-|a|≤a≤|a|，-|b|≤b≤|b|

因此，相加得：-|a|-|b|≤a+b≤|a|+|b|，即：|a+b|≤|a|+|b|

将b换成-b，即有：|a-b|≤|a|+|b|

再证||a|-|b||≤|a±b|

由于|a|=|a-b+b|≤|a-b|+|b|；|b|=|b-a+a|≤|a-b|+|a|

所以，|a|-|b|≤|a-b|，|b|-|a|≤|a-b|，即：||a|-|b||≤|a-b|

将b换成-b，即有：||a|-|b||≤|a+b|

因此，||a|-|b||≤|a±b|≤|a|+|b|

其他不等式：

①√((a?+b?)/2)≥(a+b)/2≥√ab≥2/(1/a+1/b)

②√(ab)≤(a+b)/2

③a?+b?≥2ab

④ab≤(a+b)?/4

⑤||a|-|b| |≤|a+b|≤|a|+|b|

含有两个绝对值的不等式，咋解啊

绝对值不等式是一类形如 |x| < a 或 |x| >

a 的不等式，其中 a 是实数，x 是未知数。解决绝对值不等式的关键是确定绝对值的取值范围，然后根据绝对值的定义进行分类讨论。以下将介绍两种常见的绝对值不等式的解法。1. 等效变形法

对于形如 |x| < a 的绝对值不等式，我们可以将其等效变形为 -a < x < a。也就是说，当 x 的取值在这个区间内时，|x| < a 成立。因此，求解这类不等式就转化为了求解该区间的解集。

举例来说，我们要求解 |2x + 1| < 5 的解集。根据等效变形法，我们将其变形为 -5 < 2x + 1 < 5。然后，将其化简为 -3 < x

< 2. 因此，解集为 (-3, 2)。

2. 分类讨论法

对于形如 |x| > a 的绝对值不等式，我们可以进行分类讨论。当 x > 0 时，|x| = x；当 x < 0 时，|x| = -x。因此，我们可以将原不等式分成两个不等式来讨论，分别为 x > a 和 x < -a。然后，求解这两个不等式的解集，并将它们合并起来，即为所求的解集。

举例来说，我们要求解 |x - 2| > 3 的解集。按照分类讨论法，我们将其分为两个不等式：

- x - 2 > 3，即 x > 5；

- x - 2 < -3，即 x < -1。

因此，解集为 (-∞, -1) ∪ (5, ∞)。

绝对值不等式的求解方法并不难，但要注意判断绝对值的取值范围，选择合适的解法，并合理使用等式变形和分类讨论等数学技巧。掌握这些技巧，可以更加轻松地解决各类绝对值不等式题目。

带绝对值的不等式怎么算

方法一：直接拿掉绝对值 分类取相反数

如：Ix+1I=I2x-3I

①化为x+1=2x-3

②化为x+1=-(2x-3)

方法二：左右分别平方 去掉绝对值

化为(x+1)^2=(2x-3)^2

风雨清华路为你解答

谢谢采纳~~

含绝对值的不等式恒成立问题！急！

带绝对值的不等式怎么算如下：

这个不等式表示a的绝对值不超过b。当b≥0时，原不等式等价于-b≤a≤b。这个不等式组包括了a的所有可能取值。这是因为根据绝对值的定义，我们知道|a|=a，当a≥0，|a|=-a，当a<0。因此，当a的绝对值不超过b时，a的取值范围就在-b和b之间。

当b<0时，由于绝对值的非负性，我们知道|a|≥0，因此原不等式无解。这是因为任何实数的绝对值都是非负的，不可能小于一个负数。

如下：

如果原不等式是|a|≥b的形式，我们也可以通过类似的方法转化为不带绝对值的形式。具体来说，当b≥0时，原不等式等价于a≤-b或a≥b。这个不等式组也包括了a的所有可能取值。这是因为当a的绝对值大于或等于b时，a可以取任意小于等于-b或大于等于b的实数。

当b<0时，由于绝对值的非负性，我们知道|a|≥0，因此原不等式等价于a∈R，即a可以取任意实数。这是因为任何实数的绝对值都是非负的，一定大于一个负数。

得出绝对值不等式的解法：|a|≤b<=>-b≤a≤b，当b≥0时；无解，当b<0时。|a|≥b<=>a≤-b或a≥b，当b≥0时；a∈R，当b<0时。

不等式的两边可以是任何实数或者代数式。这意味着，我们可以用不等式来表示各种数学关系，例如x^2+2x-3>0，这个不等式描述的是一个二次函数的值大于0时的x的取值范围。代数式的范围广泛，可以是多项式、分式、根号等，这使得不等式具有很强的表达力。

绝对值不等式性质及公式

方法1：展开法

当x ≤1时，|x-1|+|x-5| = 1-x+5-x = 6-2x，最小值在x=1处取得，最小值为4

当1＜x＜5时，|x-1|+|x-5| = x - 1+5-x = 4，最小值为4

当x≥5时，|x-1|+|x-5| = x-1+x-5 = 2x - 6，最小值在x=5时取得，最小值为4

所以|x-1|+|x-5|的最小值为4

只要a小于4，|x-1|+|x-5|>a 就恒成立

所以a的取值范围是 a＜4

方法2：绝对值不等式法

|x-1|+|x-5| = |x-1|+|5-x| ≥ |x-1+5-x| = 4

所以|x-1|+|x-5| ≥ 4，即|x-1|+|x-5|的最小值为4

只要a小于4，|x-1|+|x-5|>a 就恒成立

所以a的取值范围是 a＜4

绝对值不等式性质及公式如下：

性质：

1、非负性：|a|≥0。这意味着对于任意实数a，它的绝对值都是非负的。换句话说，绝对值不能是负数或零。

2、对称性：如果a和b互为相反数，那么|a|=|-b|。这是因为相反数的定义是它们的绝对值相等，而符号相反。

3、传递性：如果|a|=b，|b|=c，那么|a|=c。这意味着绝对值的等量传递性。如果两个数的绝对值相等，那么它们的绝对值也相等。

4、三角不等式：对于任意实数x和y，都有|x|-|y|≤|x±y|≤|x|+|y|。这是绝对值不等式最常用的性质之一，它帮助我们约束和估计绝对值的大小。这个不等式也被称为三角形不等式，因为它的形式与三角形两边之和大于第三边的性质类似。

公式：

1、绝对值不等式：|a|-|b|≤|a±b|≤|a|+|b|。

2、平方不等式：|a|?-|b|?≤（a±b）?≤|a|?+|b|?。

3、柯西不等式：如果a1，a2，…，an和b1，b2，…，bn都是实数，那么（a1/√b1）+（a2/√b2）+…+（an/√bn）≥（√a1?+√a2?+…+√an?）/（√b1+√b2+…+√bn）。

绝对值不等式的实际应用：

1、最值问题：在生产生活中常常会遇到求最值的问题，比如利润最大化、成本最小化等。而绝对值不等式可以用来确定这些最值存在的情况，例如在求解一元函数的最值时可以通过求导数确定函数的极值点，再利用绝对值不等式的性质确定最值。

2、数列问题：数列问题中也会涉及到绝对值不等式，例如在求解数列的极限时需要用到绝对值的性质。例如，如果一个数列的和存在极限，那么这个数列的通项的绝对值的和也应该存在极限。

3、几何问题：在几何中，绝对值不等式可以用来解决一些与距离和范围有关的问题，例如在求解两线段和的最小值时需要用到绝对值不等式的性质。例如，三角形ABC中的两边长分别为a、b，其夹角为θ，求第三边的最小长度时就需要用到绝对值不等式|A|+|B|≥|C|。

4、物理问题：在物理学中，绝对值不等式也可以用来解决一些问题，例如在求解弹性碰撞中的能量损失时需要用到绝对值不等式。例如，两个质量分别为m1和m2、速度分别为v1和v2的小球发生弹性碰撞后，其速度分别变为v1'和v2'，求解两球间最大能量损失时需要用到绝对值不等式|p|+|q|≥|p+q|。