高考函数试题分析,高考函数试题

1.高中数学函数例题以及解析？

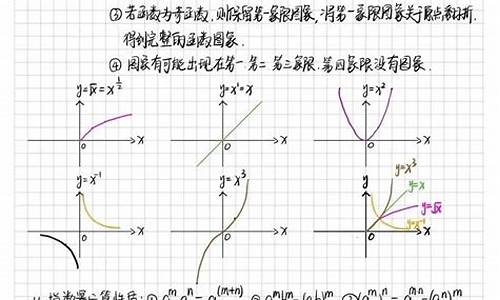
解：（1）由图像知，函数振幅为2，故A＝2

由图像知从－π/3到2π/3是半个周期，故T＝[（2π/3-(-π/3）]*2＝2π

即2π/ω=2π, 所以ω=1

所以f(x)=2sin(x+φ)

把最高点（2π/3, 2）（或最低点(-π/3,-2)）代入函数，得2=2sin(2π/3+φ)

故sin(2π/3+φ)=1

所以2π/3+φ＝π/2+2kπ（k∈Z），

即φ＝2kπ－π/6（k∈Z）

因为－π/2<φ<π/2

所以φ＝－π/6

所以f(x)=2sin(x－π/6)

(2)因f(a)=3/2, 即sin(a－π/6)=3/4

所以sin(2a+π/6)=cos[π/2 -(2a+π/6)](这里利用诱导公式cos(π/2-a)=sina)

=cos(π/3-2a)=cos(2a-π/3)(这里利用诱导公式cos(-a)=cosa)

=cos[2(a-π/6)]=1-2[sin(a-π/6)]^2 (这里利用2倍角公式）

=1-2(3/4)^2=-1/8

即sin(2a+π/6)=-1/8

高中数学函数例题以及解析？

二、 典型例题讲解:

例1.设a＞0, f (x)＝ 是R上的奇函数.

(1) 求a的值;(2) 试判断f (x )的反函数f－1 (x)的奇偶性与单调性

例2. 是否存在实数a, 使函数f (x )＝ 在区间 上是增函数? 如果存在,

说明a可以取哪些值; 如果不存在, 请说明理由.

三、历年高考题：

1.（安徽卷文7）设 ，则a，b，c的大小关系是

（A）a＞c＞b （B）a＞b＞c （C）c＞a＞b （D）b＞c＞a

2.（湖南卷文8）函数y=ax2+ bx与y= (ab ≠0，| a |≠| b |)在同一直角坐标系中的图像可能是

3.（辽宁卷文10）设 ，且 ，则

（A） （B）10 （C）20 （D）100

4.（全国Ⅰ卷理8文10）设a= 2,b=In2,c= ,则

A. a<b<c B. b<c<a C. c<a<b D . c<b<a

5.（全国Ⅰ卷理10）已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b的取值范围是

(A) (B) (C) (D)

6.（全国Ⅰ卷文7）已知函数 .若 且， ，则 的取值范围是

(A) (B) (C) (D)

7.（山东卷文3）函数 的值域为

A. B. C. D.

8.（陕西卷文7）下列四类函数中，个有性质“对任意的x>0，y>0，函数f(x)满足f（x＋y）＝f（x）f（y）”的是 [ ]

（A）幂函数 （B）对数函数 （C）指数函数 （D）余弦函数

9.（上海卷文17）若 是方程式 的解，则 属于区间 （ ）

（A）（0，1）. （B）（1，1.25）. （C）（1.25，1.75） （D）（1.75，2）

10.（四川卷文2）函数y=log2x的图象大致是

(A) (B) (C) (D)

11.（天津卷文6）设

(A)a<c<b (B) b<c<a (C) a<b<c (D) b<a<c

12.（浙江卷文2）已知函数 若 =

(A)0 (B)1 (C)2 (D)3

13.（重庆卷文4）函数 的值域是

（A） (B) (C) (D)

14.（北京卷文2）若 ，则（ ）

A． B． C． D．

15.（湖南卷文6）下面不等式成立的是( )

B C D．

16（江西卷文4）若 ，则( )

A． B． C． D．

17.（辽宁卷文4）已知 ， ， ， ，则（ ）

A． B． C． D．

18.（全国Ⅱ卷理4文5）若 ，则（ ）

A． < < B． < < C． < < D． < <

19.（山东卷文12）已知函数 的图象如图所示，则 满足的关系是（ ）

A． B．

C． D．

20.（天津卷文10）设 ，若对于任意的 ，都有 满足方程 ，这时 的取值的集合为（ ）

A． B． C． D．

21.（山东卷文15）已知 ，则 的值等于 ．

22.（重庆卷文14）若 则 ＝ .

23.（上海卷理19文19）已知函数 ．

（1）若 ，求 的值；（2）若 对于 恒成立，求实数m的取值范围．

指数函数与对数函数高考试题

1．若 ，则化简 （ ）

2． 的值所属区间是 （ ）

， ， ， ，

3． 的值是 （ ）

，

4．化简 可得 （ ）

5．已知 ， ，则 （ ）

6．已知 ，则 （ ）

7．设 （ 为大于1的整数），则 的值为 （ ）

8．与方程 同解的方程是 （ ）

9．函数 的图像大致是 （ ）

10．函数 定义在实数集 上， ，且当 时， ，则 （ ）

是奇数且在 上是单调增函数　　 是奇数且在 上是单调减函数

是偶函数且在 上是单调减函数　 是偶函数且在 上不是单调函数

11．已知 ，则函数 和 在同一坐标系中的图象只可能是图中的

12．设 ，则 （ ）

13．方程 的实数根有 （ ）

个 个 个 无数个

14．方程 的解集是 （ ）

，

15．方程 的解是

， ， ， ，

16．方程 的解为 （ ）

17．若 ，则 、 、 的大小关系是 （ ）

18．若 、 均为不等于 的正数 ，则 （ ）

19．若 ， 、 为不等于 的正数，则 （ ）

20．设 ， ，且 ，则 （ ）

21．如图，指数函数 ， ， ， 在同一坐标系中，则 ， ， ，

的大小顺序是 （ ）

22. 如图,设 ， ， ， 都是不等于 的正数,在同一坐标系中,函数 ， ， ，

的图象如图,则 ， ， ， 的大小顺序关系是 （ ）

23. 函数 的值域为 （ ）

， ， ， ，

24. 函数 （ 且 （ ）

是奇函数 是偶函数 既是奇函数又是偶函数 是非奇非偶函数

25. 已知 ，那么 的值为 （ ）

26. 不等式 的解集是 （ ）

27. 计算 （ ）

28. 函数 的定义域是 （ ）

， ， ， ， ，

29. 方程 的解集是 （ ）

， ，

30. 若 ，则 （ ）

31．方程 的解集是 （ ）

， ，

32. 下列各式成立的有

（1） ； （2） ；

（3） ； （4） .

个 个 个 个

33. 当 时，在同一坐标系中，函数 与 的图象是　　 （ ）

34. 如果 ，则在区间 ， 上函数 （ ）

是减函数且 是减函数且 是增函数且 是增函数且

35. 方程 的解集是 （ ）

， ， ，

36. 已知函数 在 ， 上递减，且 ，则 的取值范围是（ ）

且

37. 若 ，则 （ ）

38. 满足不等式 的正整数 的个数有 （ ）

个　　　　 个　　　　 个　　　　 个

39．方程 的解集是 （ ）

， ， ，

40．设 ，函数 ，则使 的 的取值范围是（ ）

， ， ， ，

41．若正整数 满足 ，则 （ ）

42. 下列不等式成立的是（ ）

43．下列不等式成立的是（ ）

44. 的值为

45. 已知函数 满足： ，则 ＝ ；当 时 ＝ ，则 ＝（ ）

46. 若 ， ，则（ ）

， ， ， ，

47. 若函数 的图象与函数 的图象关于直线 对称，则 （ ）

48. 若 ，则（ ）

典型例题答案

解：(1) 因为 在R上是奇函数, 所以 ,

(2)

, 为奇函数.

用定义法可证 为单调增函数.

解：设 , 对称轴 .

(1) 当 时, ;

(2) 当 时, . 综上所述:

历年高考题答案

1.答案A

解析 在 时是增函数，所以 ， 在 时是减函数，所以 。

2.答案D

解析对于A、B两图，| |>1而ax2+ bx=0的两根之和为 - ,由图知0<- <1得-1< <0,矛盾，对于C、D两图，0<| |<1,在C图中两根之和- <-1，即 >1矛盾，选D。

3.答案D

解析：选A. 又

4.答案C

解析 a= 2= , b=In2= ,而 ,所以a<b,

c= = ,而 ,所以c<a,综上c<a<b.

5.答案A

命题意图本小题主要考查对数函数的性质、函数的单调性、函数的值域，考生在做本小题时极易忽视a的取值范围，而利用均值不等式求得a+2b ,从而错选A,这也是命题者的用苦良心之处.

解析因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去)，或 ，所以a+2b=

又0<a<b,所以0<a<1<b，令 ,由“对勾”函数的性质知函数 在 (0,1)上为减函数，所以f(a)>f(1)=1+ =3,即a+2b的取值范围是(3,+∞).

6.答案C

命题意图本小题主要考查对数函数的性质、函数的单调性、函数的值域，考生在做本小题时极易忽视a的取值范围，而利用均值不等式求得a+b= ,从而错选D,这也是命题者的用苦良心之处.

7.答案A

解析因为 ，所以 ，故选A。

命题意图本题考查对数函数的单调性、函数值域的求法等基础知识。

8.答案C

解析因为 所以f（x＋y）＝f（x）f（y）。

9.

10.解析：本题考查对数函数的图象和基本性质.

11.答案：C

12.答案D

解析因为 ，

所以c最大，排除A、B；又因为a、b ，所以 ，故选D。

解析： +1=2，故 =1，选B，本题主要考察了对数函数概念及其运算性质，属容易题

13.答案C

解析 .

14.答案A

解析利用中间值0和1来比较:

15.答案A

解析由 , 故选A.

16.解析 函数 为增函数

17.解析本小题主要考查对数的运算。

由 知其为减函数, 答案：C

18.解析由 ，令 且取 知 < < 答案C

19.解析本小题主要考查正确利用对数函数的图象来比较大小。

由图易得 取特殊点

.选A.

20.解析易得 ，在 上单调递减，所以 ，故 选B．

21.解析本小题主要考查对数函数问题。

22.解析本小题主要考查指数的运算。

答案-23

即 ， ，

，

故 的取值范围是

23.解析（1）当 时， ；当 时，

由条件可知 ，即

解得　　　　　　　　　　　　　　　　　　

（2）当 时，

一、基本概念：

1、 数列的定义及表示方法：

2、 数列的项与项数：

3、 有穷数列与无穷数列：

4、 递增（减）、摆动、循环数列：

5、 数列{an}的通项公式an：

6、 数列的前n项和公式Sn:

7、 等差数列、公差d、等差数列的结构：

8、 等比数列、公比q、等比数列的结构：

二、基本公式：

9、一般数列的通项an与前n项和Sn的关系：an=

10、等差数列的通项公式：an=a1+(n-1)d an=ak+(n-k)d (其中a1为首项、ak为已知的第k项) 当d≠0时，an是关于n的一次式；当d=0时，an是一个常数。

11、等差数列的前n项和公式：Sn= Sn= Sn=

当d≠0时，Sn是关于n的二次式且常数项为0；当d=0时（a1≠0），Sn=na1是关于n的正比例式。

12、等比数列的通项公式： an= a1 qn-1 an= ak qn-k

(其中a1为首项、ak为已知的第k项，an≠0)

13、等比数列的前n项和公式：当q=1时，Sn=n a1 (是关于n的正比例式)；

当q≠1时，Sn= Sn=

三、有关等差、等比数列的结论

14、等差数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等差数列。

15、等差数列{an}中，若m+n=p+q，则

16、等比数列{an}中，若m+n=p+q，则

17、等比数列{an}的任意连续m项的和构成的数列Sm、S2m-Sm、S3m-S2m、S4m - S3m、……仍为等比数列。

18、两个等差数列{an}与{bn}的和差的数列{an+bn}、{an-bn}仍为等差数列。

19、两个等比数列{an}与{bn}的积、商、倒数组成的数列

{an bn}、 、 仍为等比数列。

20、等差数列{an}的任意等距离的项构成的数列仍为等差数列。

21、等比数列{an}的任意等距离的项构成的数列仍为等比数列。

22、三个数成等差的设法：a-d,a,a+d；四个数成等差的设法：a-3d,a-d,,a+d,a+3d

23、三个数成等比的设法：a/q,a,aq；

四个数成等比的错误设法：a/q3,a/q,aq,aq3 (为什么？)

24、{an}为等差数列，则 (c>0)是等比数列。

25、{bn}（bn>0）是等比数列，则{logcbn} (c>0且c 1) 是等差数列。

26. 在等差数列 中：

（1）若项数为 ，则

（2）若数为 则， ，

27. 在等比数列 中：

（1） 若项数为 ，则

（2）若数为 则，

四、数列求和的常用方法：公式法、裂项相消法、错位相减法、倒序相加法等。关键是找数列的通项结构。

28、分组法求数列的和：如an=2n+3n

29、错位相减法求和：如an=(2n-1)2n

30、裂项法求和：如an=1/n(n+1)

31、倒序相加法求和：如an=

32、求数列{an}的最大、最小项的方法：

① an+1-an=…… 如an= -2n2+29n-3

② (an>0) 如an=

③ an=f(n) 研究函数f(n)的增减性 如an=

33、在等差数列 中,有关Sn 的最值问题——常用邻项变号法求解：

(1)当 >0,d<0时，满足 的项数m使得 取最大值.

(2)当 <0,d>0时，满足 的项数m使得 取最小值。

在解含绝对值的数列最值问题时,注意转化思想的应用。

六、平面向量

1．基本概念：

向量的定义、向量的模、零向量、单位向量、相反向量、共线向量、相等向量。

2． 加法与减法的代数运算：

(1) ．

(2)若a=（ ）,b=（ ）则a b=（ ）．

向量加法与减法的几何表示：平行四边形法则、三角形法则。

以向量 = 、 = 为邻边作平行四边形ABCD，则两条对角线的向量 = + , = － , = －

且有｜ ｜－｜ ｜≤｜ ｜≤｜ ｜+｜ ｜．

向量加法有如下规律： ＋ = ＋ (交换律); +( +c)=( + )+c （结合律）;

+0= ＋(－ )=0.

3．实数与向量的积：实数 与向量 的积是一个向量。

(1)｜ ｜=｜ ｜·｜ ｜;

(2) 当 ＞0时， 与 的方向相同；当 ＜0时， 与 的方向相反；当 =0时， =0．

(3)若 =（ ），则 · =（ ）．

两个向量共线的充要条件：

(1) 向量b与非零向量 共线的充要条件是有且仅有一个实数 ，使得b= ．

(2) 若 =（ ）,b=（ ）则 ‖b ．

平面向量基本定理：

若e1、e2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量 ，有且只有一对实数 ， ，使得 = e1+ e2．

4．P分有向线段 所成的比：

设P1、P2是直线 上两个点，点P是 上不同于P1、P2的任意一点，则存在一个实数 使 = ， 叫做点P分有向线段 所成的比。

当点P在线段 上时， ＞0；当点P在线段 或 的延长线上时， ＜0；

分点坐标公式：若 = ； 的坐标分别为（ ）,（ ）,（ ）；则 （ ≠－1）， 中点坐标公式： ．

5． 向量的数量积：

（1）．向量的夹角：

已知两个非零向量 与b，作 = , =b,则∠AOB= （ ）叫做向量 与b的夹角。

（2）．两个向量的数量积：

已知两个非零向量 与b，它们的夹角为 ，则 ·b=｜ ｜·｜b｜cos ．

其中｜b｜cos 称为向量b在 方向上的投影．

（3）．向量的数量积的性质：

若 =（ ）,b=（ ）则e· = ·e=｜ ｜cos (e为单位向量);

⊥b ·b=0 （ ，b为非零向量）;｜ ｜= ;

cos = = ．

(4) ．向量的数量积的运算律：

·b=b· ;( )·b= ( ·b)= ·( b);( ＋b)·c= ·c+b·c．

6.主要思想与方法：

本章主要树立数形转化和结合的观点，以数代形，以形观数，用代数的运算处理几何问题，特别是处理向量的相关位置关系，正确运用共线向量和平面向量的基本定理，计算向量的模、两点的距离、向量的夹角，判断两向量是否垂直等。由于向量是一新的工具，它往往会与三角函数、数列、不等式、解几等结合起来进行综合考查，是知识的交汇点。

七、立体几何

1.平面的基本性质：掌握三个公理及推论，会说明共点、共线、共面问题。

能够用斜二测法作图。

2.空间两条直线的位置关系：平行、相交、异面的概念；

会求异面直线所成的角和异面直线间的距离；证明两条直线是异面直线一般用反证法。

3.直线与平面

①位置关系：平行、直线在平面内、直线与平面相交。

②直线与平面平行的判断方法及性质,判定定理是证明平行问题的依据。

③直线与平面垂直的证明方法有哪些？

④直线与平面所成的角：关键是找它在平面内的射影，范围是{00.900}

⑤三垂线定理及其逆定理：每年高考试题都要考查这个定理. 三垂线定理及其逆定理主要用于证明垂直关系与空间图形的度量.如：证明异面直线垂直，确定二面角的平面角，确定点到直线的垂线.

4.平面与平面

(1)位置关系：平行、相交，（垂直是相交的一种特殊情况）

(2)掌握平面与平面平行的证明方法和性质。

(3)掌握平面与平面垂直的证明方法和性质定理。尤其是已知两平面垂直，一般是依据性质定理，可以证明线面垂直。

(4)两平面间的距离问题→点到面的距离问题→

(5)二面角。二面角的平面交的作法及求法：

①定义法，一般要利用图形的对称性；一般在计算时要解斜三角形；

②垂线、斜线、射影法，一般要求平面的垂线好找，一般在计算时要解一个直角三角形。

③射影面积法，一般是二面交的两个面只有一个公共点，两个面的交线不容易找到时用此法?

回